ДВИЖЕНИЕ ТЕЛА БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ. РЕШЕНИЕ НА КОМПЬЮТЕРЕ
Рассмотрим алгоритм решения данной задачи без учета сопротивления. Решение задачи с учетом сопротивления предлагаю провести самостоятельно. Алгоритм решения задачи будет иметь вид.
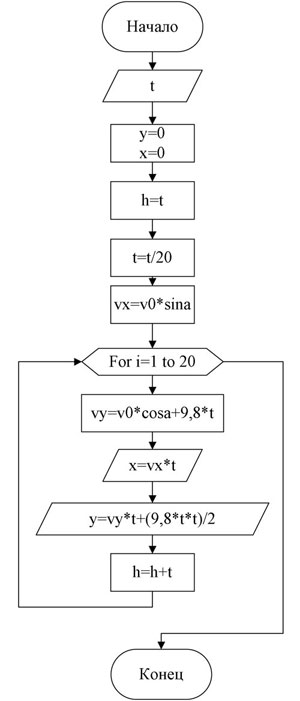
Рассмотрим ее реализацию в MS Excel. В задаче будут использоваться скрипты VBA. Первый лист выглядит, как показано на рисунке.
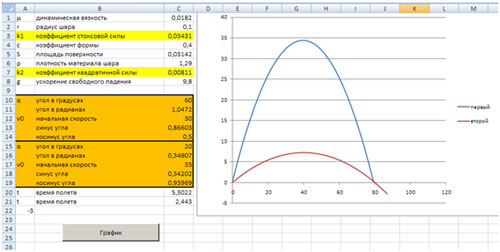
Кнопка график строит график функции согласно следующему коду на VBA.
Sub график()
Range(Cells(1, 4), Cells(100, 7)) = "" 'очищает диапазон ячеек
tper = Cells(20, 3) 'в переменую записываем первое время полета
tvtor = Cells(20, 3) 'в переменую записываем второе время полета
If tper < tvtor Then
t = tper / 20
n = (tvtor / t) + 1
Else
t = tvtor / 20
n = (tper / t) + 1
End If 'задаем шаг функции и число шагов
vxperv = Cells(12, 3) * Cells(14, 3) 'записываем скорость первого тела по x
vxvtor = Cells(17, 3) * Cells(19, 3) 'записываем скорость второго тела по x
h = t 'в переменную записываем шаг функций
Cells(1, 4) = 0
Cells(1, 5) = 0
Cells(1, 6) = 0
Cells(1, 7) = 0 ' записываем начальные условия
hyperv = 100
hvtor = 100
For i = 1 To n
vyperv = Cells(12, 3) * Cells(13, 3) - (Cells(8, 3) * h) ' первая скорость по y
vyvtor = Cells(17, 3) * Cells(18, 3) - (Cells(8, 3) * h) ' вторая скорость по y
If hyperv >= Cells(22, 1) Then
Cells(i + 1, 4) = (vxperv * h)
End If
If hyvtor >= Cells(22, 1) Then
Cells(i + 1, 6) = (vxvtor * h)
End If
hyperv = (vyperv * h) + ((Cells(8, 3) * h * h) / 2) 'высота первого
hyvtor = (vyvtor * h) + ((Cells(8, 3) * h * h) / 2) 'высота второго
If hyperv >= Cells(22, 1) Then
Cells(i + 1, 5) = hyperv
End If
If hyvtor >= Cells(22, 1) Then
Cells(i + 1, 7) = hyvtor
End If
h = h + t
Next i
End Sub