ДВИЖЕНИЕ ТЕЛА БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Рассмотрим эту известную задачу с учетом сопротивления воздуха. Будучи брошенным под углом ? к горизонту с начальной скоростью v0, тело летит, если не учитывать сопротивления воздуха, по параболе, и через некоторое время падает на землю. Напомним элементарное решение этой задачи. Разложим скорость на горизонтальную и вертикальную составляющие:
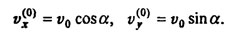
Поскольку движение по вертикали происходит под действием постоянной силы тяжести, то оно является равнозамедленным до достижения верхней точки на траектории и равноускоренным - после нее; движение же по горизонтали является равномерным. Из формул равноускоренного движения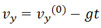 
; раз в верхней точке vy = 0, то время достижения верхней точки на траектории
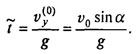
Высота этой точки
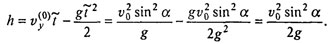
Полное время движения до падения на землю 2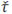
; за это время, двигаясь равномерно вдоль оси х со скоростью , тело пройдет путь
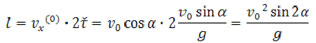
Для нахождения траектории достаточно из текущих значений x и у исключить t:
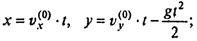
следовательно,
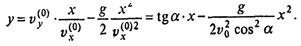
Полученное уравнение - уравнение параболы.
Полученные формулы могут, в частности, послужить для тестирования будущей компьютерной программы. При достаточно большой начальной скорости сопротивление воздуха может значительно изменить характер движения. Прежде чем выписывать уравнения, вновь оценим, какая из составляющих силы сопротивления - линейная или квадратичная по скорости - дает больший вклад в эту силу, и нельзя ли одной из этих составляющих пренебречь. Оценку проведем для шарика; по порядку величины оценка не зависит от формы тела. Итак, шарик радиусом r ? 0,1 м, движущийся со скоростью ~ 1 м/с, испытывает в воздухе линейную (стоксову) силу сопротивления
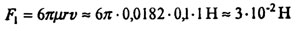
и квадратичную силу сопротивления
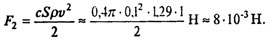
Величины F1 и F2 сопоставимые (как принято говорить, «одного порядка», так как они различаются менее, чем в 5 раз). При увеличении размера тела F2 растет быстрее, чем F1 (F1 ~ r, F2 ~ r2), при увеличении скорости F2 также растет быстрее, чем F1 (F1 ~ v, F2 ~ v2). Таким образом, если мы моделируем движение брошенного мяча, камня, то необходимо в уравнениях удерживать обе составляющие силы сопротивления, но если мы захотим моделировать полет снаряда, выпущенного из орудия, где скорость полета почти на всем его протяжении сотни метров в секунду, то линейной составляющей силы сопротивления можно пренебречь. Проецируя уравнение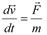 
на оси х и у, получаем
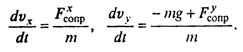
Поскольку в каждой точке траектории сила сопротивления направлена по касательной к траектории в сторону, противоположную движению, то
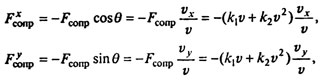
где ? - угол между текущим направлением скорости и осью х. Подставляя это в уравнение и учитывая, что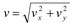 
, получаем уравнения движения в переменных vx, vy
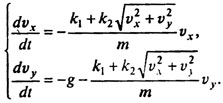
Поскольку представляет несомненный интерес и траектория движения, дополним систему еще двумя уравнениями
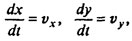
и, решая их совместно, будем получать разом четыре функции: vx(t), vy(t), x(t), y(t).